

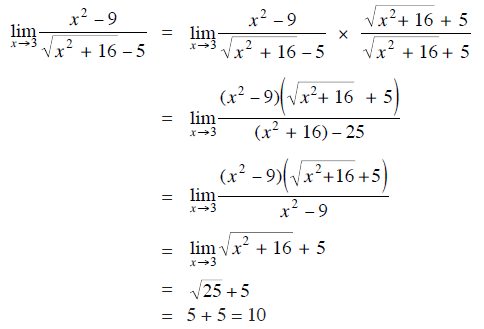
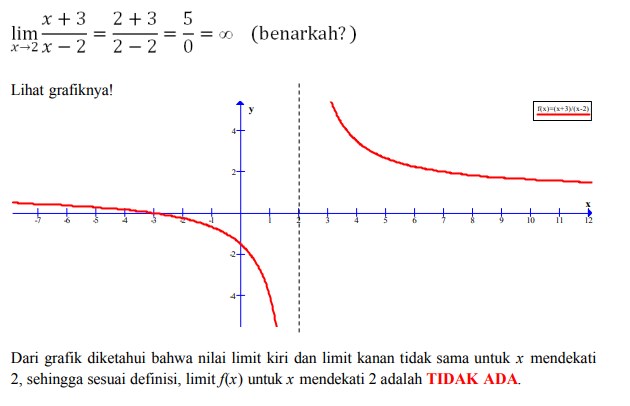
The actual image 1 Lim X Mendekati 0 Tan X Sin X X 3cos X 2 Lim X is only regarding gorgeous test if you like the about make sure you choose the original image. We all get best a great deal of Nice reading 1 Lim X Mendekati 0 Tan X Sin X X 3cos X 2 Lim X interesting photo but we solely show this articles that any of us consider are classified as the finest articles. Lim X Mendekati 0 Dari X Cos 2 6x 1 Sin 3x Tan 2 2x Brainly Co IdĪnd here is an index of image 1 Lim X Mendekati 0 Tan X Sin X X 3cos X 2 Lim X very best After merely placing syntax we possibly can one Article to as much completely readers friendly versions as you like that people inform and present Creating stories is a rewarding experience for your requirements.

Click here👆to get an answer to your question ️ limit x→0 tanx sinx x^3 = solve study textbooks guides. while the third function is continuous so. and using the trigonometric identity: sin2α = 1 −cos2α 2. Tanx − sinx x3 = ( sinx x)( 1 − cosx x2)( 1 cosx) we can use now the well known trigonometric limit: lim x→0 sinx x = 1. when x approaches 0, t = 4x approaches 0, so that lim x→0 sin 4 x 4 x = lim t→0 sin t t. Lim x→0 (1 cos x) x = lim x→0 * lim x→0 = (1) (0 2) = 0 we have used the theorem: lim x→0 = 1 example 2 find the limit limx→0 sin 4 x 4 x solution to example 2: let t = 4x. share cite follow edited at 16:12 answered at 16:07 sri amirthan theivendran 30.1k 4 24 63 add a comment. 3 note that tan 2 ( 3 x) x 2 = 1 cos 2 ( 3 x) ( 3 sin 3 x 3 x) 2 = 9 cos 2 ( 3 x) ( sin 3 x 3 x) 2 and use your knowledge of well known limits and limit laws namely lim u → 0 sin u u = 1. needless to say that the above approach uses heavy algebraic manipulation and expresses the given problem as equivalent of 4 tough limit problems (1), (2), (5), (6). In the above solution we make use of the following limits lim x → 0sinx − x x3 = − 1 6, lim x → 0tanx − x x3 = 1 3 which are easily evaluated via one application of l'hospital's rule. Lim X Mendekati 0 Tan 3x Tan 3x Cos 2x Per 4x 3 Fast Resp Ya Thnks


 0 kommentar(er)
0 kommentar(er)
